Иллюстрированный самоучитель по Mathematica
Диалог с системой и ее входной язык
Интересно отметить, что, родившись как программа для профессионалов, Mathematica в последние годы упорно позиционируется фирмой Wolfram как система, перспективная не только для высшего, но и для школьного образования. Диалог с системой идет по методу «задал вопрос — получил ответ». Не считая отдельных мелочей, такой диалог вполне понятен не только опытному математику, но и успевающему студенту и даже школьнику.
Впрочем, уже из приведенных простейших примеров видны определенные тонкости записи входных выражений, которые определяются совокупностью правил их ввода, то есть синтаксисом входного языка системы, или (более строго) языка программирования системы. Он будет рассмотрен по мере описания возможностей систем класса Mathematica. Обширные возможности этих систем в решении математических задач придают им функции не только суперкалькуляторов, но и мощных электронных справочников по математике и математическим расчетам.
Даже интуитивно ясно, что осуществление символьных операций — процесс намного более тонкий и сложный, чем реализация даже сложных численных расчетов. В какой-то степени он противен сущности вычислений, реализуемых в современных ЭВМ, — как известно, они работают с «голыми» цифрами и являются «числодробилками». Эти операции сложнее и обычных (довольно примитивных) строковых операций, используемых при обработке текстов. К тому же известно, что одни только таблицы производных, интегралов и формул преобразований занимают многие тома объемных книг. Поэтому высокая эффективность символьных операций реальна только при их реализации на современных высокопроизводительных ПК. Не случайно системы символьной математики получили серьезное развитие лишь в последний десяток лет.
Все сказанное ведет к необходимости символьного представления чисел и использования особых алгоритмов для выполнения операций с ними. Естественно, что реализация символьных операций вначале обеспечивалась за счет снижения эффективности численных расчетов.
Тем более приятно, что в новейшей системе Mathematica 4 эта порочная тенденция была решительно остановлена — данная версия системы имеет не только превосходные возможности в части символьных вычислений, но и повышенную эффективность и скорость численных расчетов. Это выдвигает систему Mathematica 4 в число лучших универсальных систем компьютерной математики.
Операции с целыми числами
Продолжим знакомство с возможностями системы Mathematica 4 примерами работы с целыми числами. Несколько таких примеров приведено на рис. 1.4.
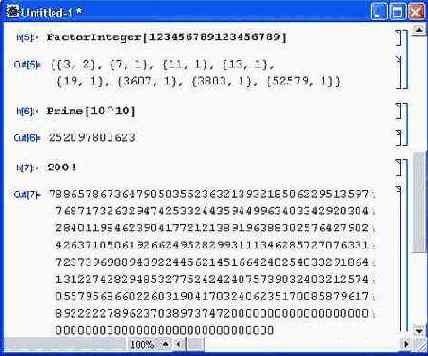
Рис. 1.4. Примеры целочисленных операций
Первая из приведенных операций дает разложение целого числа на простые множители с помощью функции Factorlnteger. Они представлены списками (в фигурных скобках) из двух чисел. Первое число — это множитель, а второе — число его повторений. В считанные секунды Mathematica 4 находит десятибиллионное простое число с помощью функции Prime. Другой характерный пример целочисленных операций — вычисление факториалов (вы можете запросто получить факториал 10 000, но ради сокращения места при описании примера в нем вычислено значение 200! Последний пример показывает отсутствие ошибок при работе с большими целыми числами — и это несмотря на то, что при его выполнении и впрямь дважды вычисляется факториал числа 10 000.
Операции с целыми числами выполняются абсолютно точно. При этом число цифр не ограничено (в разумных пределах).
Арифметика произвольной точности
Арифметика произвольной точности — еще одна из областей применения систем символьной математики (рис. 1. 5).
