Иллюстрированный самоучитель по Mathematica
Улучшенные математические возможности
Математические возможности системы Mathematica 4 существенно пополнены и улучшены. В частности, обеспечены следующие возможности:
- прямая поддержка линейной алгебры разреженных матриц;
- экспериментальная поддержка кванторного исключения с использованием цилиндрического алгебраического разложения;
- экспериментальная поддержка символьной оптимизации;
- быстрая свертка и корреляция для массивов любого размера и размерности;
- новые улучшенные алгоритмы для преобразований Фурье (рис. 1.23);
- ускоренное вычисление полиномиальных уравнений;
- новые алгоритмы для функции минимизации FindMinimum;
- расширение возможностей матричных преобразований;
- алгебраическая вычислительная поддержка для функций символьных преобразований Simplify, FunctionExpand и связанных с ними других функций;
- расширение возможностей функций преобразования FullSimplify и FunctionExpand;
- упрощение полиномиальных и других неравенств;
- полная улучшенная поддержка символьных преобразований Лапласа и Фурье;
- расширенные возможности решения трансцендентных уравнений;
- ускоренное неоднократное дифференцирование;
- поддержка ряда новых специальных функций (Дирака, Струве, обобщенных логарифмов, двумерных гипергеометрических функций Аппеля, полилогарифмов Ньелсена, гармонических функций, различных констант и т. д.);
- новые оптимизированные методы для оценивания е, n и других констант с очень высокой точностью;
- полная поддержка для непрерывных дробей и периодических цифровых последовательностей ;
- прямая поддержка поразрядных операций.
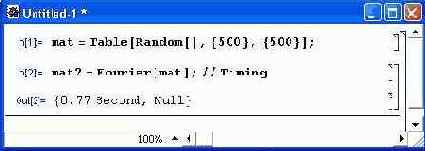
Рис. 1.23. Пример выполнения преобразования Фурье в среде Mathematica 4
Из рис. 1.23. видно, что на преобразование Фурье массива 500x500 элементов Mathematica 4 затратила около 2 с. Для сравнения отметим, что Mathematica 3 выполнила ту же работу за 11 с, то есть ускорение преобразования Фурье оказывается более чем пятикратным.
Рисунок 1.24. иллюстрирует возможности выполнения интегральных преобразований Лапласа и Фурье в символьном виде.
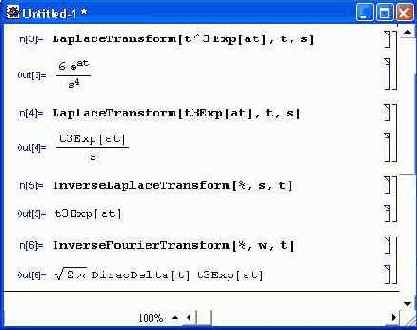
Рис. 1.24. Примеры интегральных аналитических преобразований
Некоторые другие примеры использования, характерные для системы Mathematica 4, можно найти на Интернет-странице фирмы Wolfram.
