Иллюстрированный самоучитель по Mathematica
Численные расчеты — пакет NumericalMath
Пакет расширения NumericalMath содержит множество полезных функций для тех, кто имеет дело с численными расчетами. В их числе функции для выполнения высокоточных аппроксимаций рациональными функциями, численного интегрирования и дифференцирования, вычисления пределов функций, решения уравнений, разложения в ряд и т. д. Ниже описано подавляющее большинство функций этого расширения. Исключены лишь отдельные функции, представляющие ограниченный интерес и несложные для самостоятельного изучения (в подпаке-mах Butcher, Microscope и ComputerArithmetic).
Аппроксимация аналитических функций — Approximations
Подпакет Approximations содержит ряд функций для улучшенной рациональной аппроксимации аналитических функций. Для рациональной интерполяции и аппроксимации функций по заданным значениям абсцисс служит следующая функция:
- Rationallnterpolation [f, {x,m, k}, {x 1 , x 2 , ...,.x m+k+1 } ] — возвращает аппроксимирующее функцию f выражение в виде отношения полиномов а степенью полинома числителя m и знаменателя k в абсциссах, заданных списком {x l ,x 2 ,...,x m+jt+1 }.
Пример применения этой функции:
<<NumericalMath `Approximations`
ril = Rationallnterpolation[ Exp[x], {х, 2, 4}, {0, 1/3, 2/3, 1, 4/3, 5/3, 2}]
Построим график погрешности аппроксимации, то есть график разности функ ии ril и Ехр [х] — он представлен на рис. 11.22.
Нетрудно заметить, что если в центральной части области аппроксимации погрешность мала (менее 5-10- 7 ), то у правого края она резко возрастает.
Представленная функция может использоваться и в иной форме:
Rationallnterpolation[f,{х, m, k},{x, xmin, xmax}]
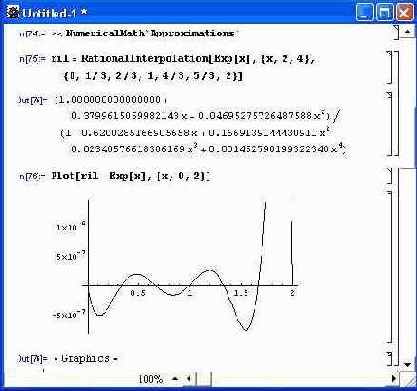
Рис. 11.22. График погрешности рациональной аппроксимации экспоненциальной функции
В данном случае выбор абсцисс осуществляется автоматически в интервале от xmin до mах. В отличие от первого случая, когда абсциссы могли быть расположены неравномерно, в данном случае расположение их будет равномерным. Приведем пример аппроксимации функции синуса в интервале от n до n:
ri2 = RationalInterpolation[Sin[x],{x,3,4},{x,-Pi,Pi}]
Интересно оценить погрешность аппроксимации. Для этого достаточно построить график разности аппроксимирующей и аппроксимируемой функций. Это построение представлено на рис. 11.23. Любопытно, что хотя максимальная погрешность и значительна, резких выбросов погрешности в данном случае нет.
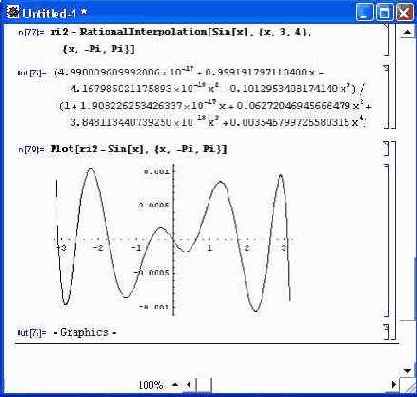
Рис. 11.23. График погрешности аппроксимации синусоидальной функции
При рациональной аппроксимации можно задать опции WorkingPrecision и Bias со значениями по умолчанию $MachinePrecision и 0 соответственно. Опция Bias обеспечивает автоматическую расстановку узлов интерполяции. При Bias->0 обеспечивается симметрирование выбросов погрешности, дающее наименьшее ее значение в пиках. Ниже приведен пример интерполяции (аппроксимации) экспоненциальной функции в интервале изменения х от 0 до 2:
ri3 = RationalInterpolation[Exp[x],{x,2,4},{x,0,2},Bias->.25]
Построение графика погрешности (рис. 11.24) показывает, что правильным выбором центра интерполяции можно существенно уменьшить ее погрешность. Теперь большая погрешность наблюдается в левой части графика. Однако резкого выброса погрешности в данном случае нет.
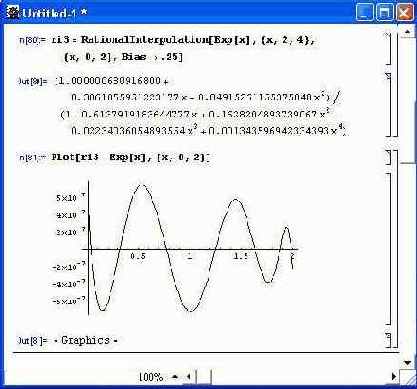
Рис. 11.24. Погрешность аппроксимации экспоненты при выборе опции Bias->.25
Из приведенных примеров ясно, что рациональная аппроксимация способна дать существенное уменьшение погрешности при некотором оптимальном расположении узлов аппроксимации и выравнивании погрешностей по абсолютной величине в точках минимумов и максимумов кривой погрешности. Это лежит в основе так называемой минимаксной аппроксимации. Она реализуется следующей функцией:
- MiniMaxApproximation[f,{x,{xmin,xmax},m,k}] — возвращает рациональную функцию минимаксной аппроксимации f при степени полиномов числителя и знаменателя {m, k} ив интервале изменения х от xmin до xmax:
- MiniMaxApproximation [f, approx, {x, {xmin, xmax} ,m, k} ] —возвращает рациональную функцию минимаксной аппроксимации f при степени полиномов числителя и знаменателя {m, k} ив интервале изменения х от xmin до xmax с возможностью выбора метода аппроксимации approx.
Они начинаются с первого шага, на котором используется функция Rational Interpolation. Затем аппроксимация последовательно улучшается применением алгоритма Ремеза, лежащего в основе этого вида аппроксимации.
Функция MiniMaxApproximation возвращает два списка — первый с координатами абсцисс, при которых наблюдается максимальная погрешность, второй содержит рациональную функцию аппроксимации. Ниже представлен пример аппроксимации экспоненциальной функции:
mmlist = MiniMaxApproximation[Ехр[х], {х, {0, 2}, 2, 4}]
Выделим формулу аппроксимации:
mmfunc = mmlist[[2, 1]]
Теперь можно построить график погрешности аппроксимации (рис. 11.25).
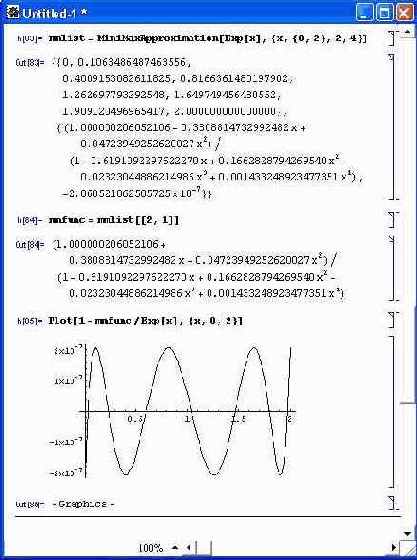
Рис. 11.25. График погрешности при минимаксной аппроксимации экспоненциальной функции
Следует отметить, что малость абсолютной ошибки для ряда функций (например, тригонометрических) может приводить к большим относительным погрешностям в точках, где функции имеют нулевые значения. Это может привести к отказу от выполнения аппроксимации вследствие исчерпания числа итераций (опция Maxlterations по умолчанию имеет значение 20). Такой случай наблюдается, например, при исполнении следующей команды:
MiniMaxApproximation[Cos[x], {х, {1, 2}, 2, 4}]
Делением функции на (x-Pi/2) можно исключить эту ситуацию:
MiniMaxApproximation[Cos[x]/(x-Pi/2),{*,{1!,2},2,4}] [[2,1]]
График погрешности для этого примера представлен на рис. 11.26. Обратите внимание на то, что в этом примере погрешность аппроксимации не превышает (б...7)-10- 10 .
В приложении дан список функций общей рациональной интерполяции (аппроксимации) для аналитических зависимостей, заданных параметрически. Примеры применения этого довольно редкого вида аппроксимации можно найти в справочной базе данных системы Mathematica. Там же можно найти дополнительные соображения по уменьшению погрешности аппроксимации.
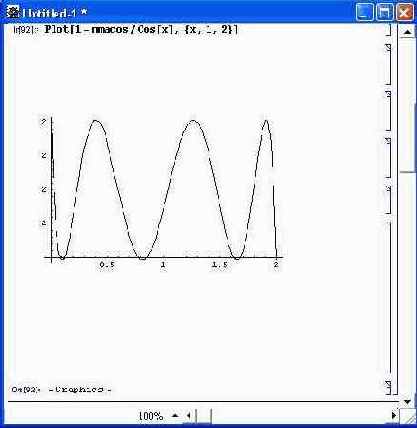
Рис. 11.26. График погрешности при минимаксной аппроксимации функции косинуса
