Иллюстрированный самоучитель по Mathematica
Графы и их функции
Mathematica имеет самые обширные возможности решения задач, связанных с графами. Задание графов и манипуляции с ними также включены в пакет комбинаторики. Они представлены четырьмя группами функций.
|
Представление графов |
||
|
AddEdge |
AddVertex |
Breadth'FirstTraversal |
|
ChangeEdges |
ChangeVertices |
CircularVertices |
|
CompleteQ |
Contract |
DeleteEdge |
|
DeieteVertex |
DepthFirstTr aversal |
Diameter |
|
DilateVertices |
Distribution |
Eccentricity |
|
Edges |
EmptyQ |
FromAd j acencyLists |
|
FromOrderedPairs |
FromUnorderedPairs |
GraphCenter |
|
GraphComplement |
InduceSubgraph |
M |
|
MakeSimple |
MakeUndirected |
Normal! zeVerticesPointsAndLines |
|
Pseudograph |
RadialEmbedding |
Radius |
|
RankGraph |
RankedEmbedding |
ReadGraph |
|
RemoveSelf Loops |
RootedEmbedding |
RotateVertices |
|
ShakeGraph |
ShowGraph |
ShowLabe 1 edGr aph |
|
SimpleQ |
Spectrum |
SpringErrbedding |
|
ToAdjacencyLists |
ToOrderedPairs |
ToUnorderedPairs |
|
TranslateVertices |
UndirectedQ |
UnweightedQ |
|
Vertices |
WriteGraph |
|
Одной из самых важных функций этой группы является функция ShowGraph (показать граф). Она обеспечивает визуальное представление графа, заданного аргументом функции. Покажем работу избранных функций этой группы на нескольких примерах.
На рис. 11.7 показано построение полного графа и его таблицы. Параметром графа является число 6, характеризующее число узловых точек графа, соединенных друг с другом.
Изменяя значение параметра графа, можно получить множество других графов. На рис. 11.8 показан вид двух разных графов. Верхний граф — многолучевая звезда с добавленным отрезком, полученная с помощью функции AddEdge. Первый аргумент задает исходный граф (в нашем случае — звезду с 11 узлами), а второй — соединяемые отрезком прямой точки. Нижний рисунок иллюстрирует построение подграфа.
Еще пара графов представлена на рис. 11.9. Этот рисунок иллюстрирует применение функций Contract и GridGraph.
Последняя из них строит сеточный граф.
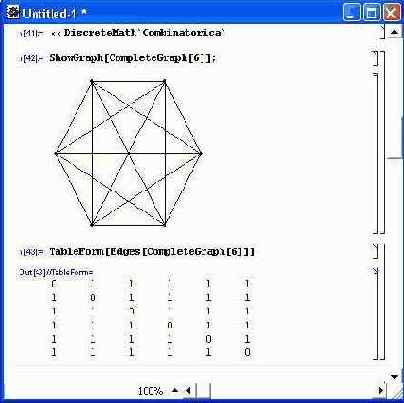
Рис. 11.7. Пример построения полного графа и его таблицы
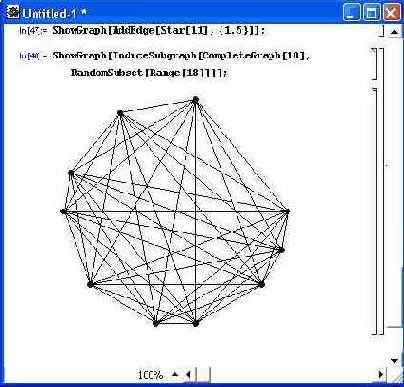
Рис. 11.8. Построение графа звезды и подграфа
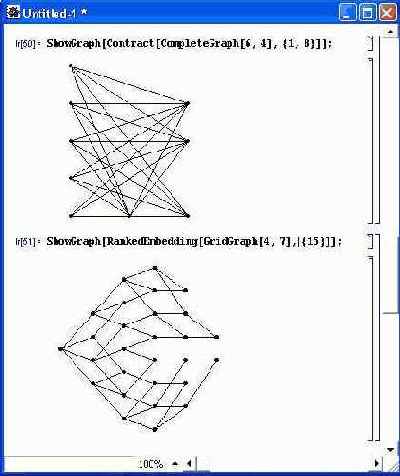
Рис. 11.9. Примеры построения графов с помощью функций Contractn GridGraph
Приведенный выше набор функций позволяет строить практически любые виды графов и обеспечивает высокую степень их визуализации.
|
Создание графов
|
||
|
CartesianProduct
|
CirculantGraph
|
CodeToLabeledTree
|
|
CompleteGraph
|
Cycle
|
DegreeSequence
|
|
EmptyGraph
|
ExactRandomGraph
|
ExpandGraph
|
|
Functional-Graph
|
GraphDif ference
|
Graphlnter section
|
|
GraphJoin
|
GraphPower
|
GraphProduct
|
|
GraphSum
|
GraphUnion
|
GraphicQ
|
|
GridGraph
|
Hypercube
|
IncidenceMatrix
|
|
IntervalGraph
|
LabeledTreeToCode
|
LineGraph
|
|
MakeGraph
|
NthPair
|
Path
|
|
RandomGraph
|
RandomTree
|
RandomVertices
|
|
RealizeDegreeSequence
|
RegularGraph
|
RegularQ
|
|
Turan
|
Wheel
|
-
|
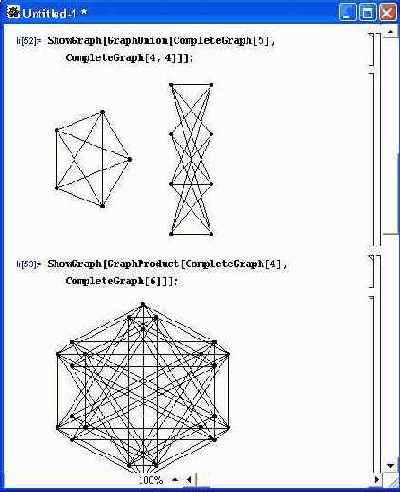
Рис. 11.10. Создание графов с помощью функций GraphUnion и GraphProduct С действием других функций нетрудно ознакомиться самостоятельно.
|
Свойства графов
|
||
|
ArticulationVertices
|
Automorphisms
|
Bi Connected Components |
|
BiconnectedQ
|
BipartiteQ
|
Bridges
|
|
ChromaticNumber
|
Chromatic Polynomial |
CliqueQ
|
|
Connected Components |
ConnectedQ
|
DeBruijnSequence
|
|
DeleteCycle
|
EdgeChromatic Number |
EdgeColoring
|
|
EdgeConnectivity
|
Element
|
EulerianCycle
|
|
EulerianQ
|
ExtractCycles
|
FindCycle
|
|
Girth
|
GraphPower
|
HamiltonianCycle
|
|
HamiltonianQ
|
Harary
|
HasseDiagram
|
|
IdenticalQ
|
Independent SetQ
|
IsomorphicQ
|
|
Isomorphism
|
IsomorphismQ
|
MaximumClique
|
|
Maximum lndependentSet |
Minimum VertexCover |
OrientGraph
|
|
PartialOrderQ
|
PerfectQ
|
SelfComplementaryQ
|
|
StronglyConnected Components |
TopologicalSort
|
TransitiveClosure
|
|
TransitiveReduction
|
TravelingSalesman
|
TravelingSalesman Bounds |
|
TreeQ
|
Trianglelnequality
|
TwoColoring
|
|
VertexColoring
|
VertexConnectivity
|
VertexCoverQ
|
|
WeaklyConnected Components |
||
Рисунок 11.11 (сверху) показывает применение функции OrientGraph для построения ориентированного графа, который представляется стрелками. Там же (снизу) показано применение функции ShowLabeledGraph для построения графа с маркированными числами вершинами. Напомним, что функция ShowGraph позволяет наблюдать графы без маркировки вершин.
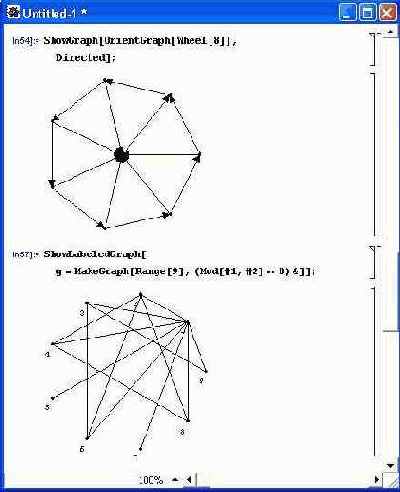
Рис. 11.11. Построение графов — ориентированного (сверху) и с маркированными вершинами (снизу)
Построение широко используемой в теории графов диаграммы Хассе (Hasse) иллюстрирует рис. 11.12.
|
Алгоритмическая теория графов
|
||
|
AllPairsShor test Path |
BipartiteMatchin
|
Cofactor |
| Dijkstra | FindSet | GraphPower |
| InitializeUnionFind | Maxima IMatching | MaximumAntichain |
| MaximumSpanningTree | MinimumChainPartition | MinimumSpanningTree |
| NetworkFlowEdges | Networks' low | NumberOfSpanningTrees |
| PathConditionGraph | PlanarQ | Shortest PathSpanningTree |
| ShortestPath | StableMarriage | UnionSet |
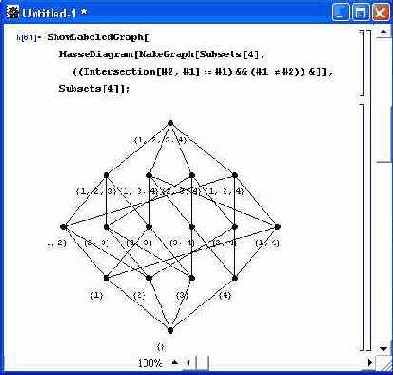
Риc. 11.12. Построение диаграммы Хассе
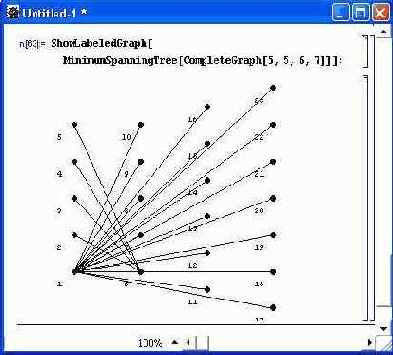
Риc. 11.13. Пример применения функции MinimumSpanningTree
В целом следует отметить, что набор функций в области создания, визуализации и теории графов весьма представителен, так что специалисты в области графов могут найти в этом наборе как типовые, так и уникальные средства.
