Иллюстрированный самоучитель по Mathematica
Нелинейная регрессия — NonlinearFit
В подпакете NonlinearFit содержатся функции для выполнения нелинейной регрессии общего вида:
- NonlinearFit[data,model,variables,parameters] — выполняет регрессию по заданной модели (формуле) model с переменными variables и параметрами parameters для заданных данных data;
- NonlinearRegress[data,model,variables,parameters] —выполняет регрессию по заданной модели (формуле) model с переменными variables и параметрами parameters для заданных данных data с выдачей списка диагностики.
Данные могут быть представлены списком ординат {у1,у2,...} или списком {{x11,x12,..., yl}, {х21, х22,..., у2},...}. В ходе регрессии минимизируются заданные параметры, так что заданная модель регрессии приближает данные с минимальной среднеквадратичной погрешностью.
На рис. 12.7 показан пример выполнения логарифмической регрессии. При ней модель представлена выражением a*Log[b*x]. Результатом действия функции NonlinearFit является уравнение регрессии в виде этой модели с найденными значениями параметров а и Ь. Представлена также визуализация регрессии в виде графика функции-модели и исходных точек. Следует отметить, что реализация нелинейной регрессии разными методами может давать заметно различающиеся результаты, так что представленные результаты не являются абсолютно строгими.
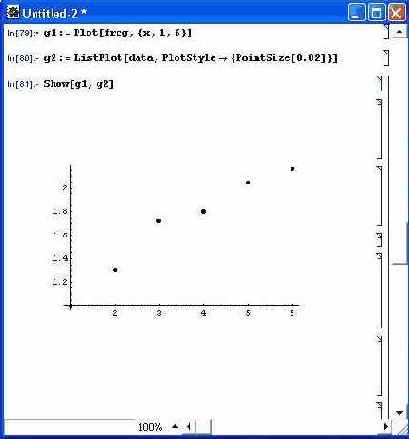
Рис. 12.7. Пример логарифмической регрессии
Применение функции NonlinearRegress иллюстрирует следующий пример:
NonlinearRegress [data, a*Log[b*x] ,{x},{a,b}]
{BestFitParameters -> {a -> 0.665503, b -4 4. 11893},
ParameterCITable ->
Estimate Asymptotic SE CI
a 0.665503 0.0504167 {0.525524, 0.805482},
b 4.11893 0.806289 {1.88031, 6.35754}
EstimatedVariance -> 0 . 00558058,
DF SumOfSq MeanSq
Model 2 17.7425 8.87126
ANOVATable ->
Error 4 '0.0223223 0.00558058,
Uncorrected Total 6 17.7648
Corrected Total 5 0.994689
1. -0.972212 AsymptoticCorrelationMatrix ->
Curvature
Max Intrinsic 2 . 94314 x lO'16,
FitCurvatureTable -» }
Max Parameter-Effects 2.07792
95. % Confidence Region 0.379478
Как нетрудно заметить, в данном случае выдается отчет о проведении регрессии. Более детальные данные об опциях и обозначениях в отчетах нелинейной регрессии можно найти в справочной базе данных.
Полиномиальная регрессия — PolynomialFit
К сожалению, средства регрессии в Mathematica разбросаны по разным пакетам. Так, в подпакете PolynomialFit пакета NumericalMath определена функция для полиномиальной регрессии:
- PolynomialFit [data, n] — возвращает полином степени п, обеспечивающий наилучшее среднеквадратичное приближение для данных, представленных параметром data. Если data является списком ординат функции, то абсциссы формируются автоматически с шагом 1. Если data является списком координат {xi,yi}, то полином наилучшим образом приближает зависимости
<<NumericalMath`PolynomialFit`
р = PolynomialFit[{l,3.9,4.1,8.9,16,24.5,37,50},3]
FittingPolyncmial [ <> , 3]
p[5]
15.8727
Expand[p[x]]
2.35-1.44066x+0.659848x2 +0.0338384x3
Другой пример с построением графиков исходных точек и аппроксимирующего полинома дан на рис. 12.8.
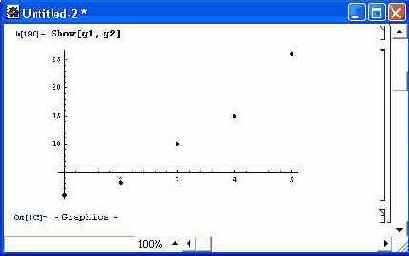
Рис. 12.8. Графики точек исходной зависимости и аппроксимирующего полинома
Нетрудно заметить, что точки исходной зависимости неплохо (но не точно) укладываются на график полинома.
Сплайн-регрессия — SplineFit
Сплайны представляют собой набор полиномов невысокой степени, последовательно применяемых к наборам точек аппроксимирующей функции. Чаще всего используется кубическая сплайновая аппроксимация, при которой коэффициенты полиномов выбираются из условий равенства в стыкуемых точках не только значений функции, но также первой и второй производных. Это придает графику сплайна вид плавной кривой, точно проходящей через узловые точки и напоминающей изгибы гибкой линейки (spline в переводе — гибкая линейка).
Подпакет SplineFit пакета NumericalMath содержит функцию для проведения сплайн- регрессии, при которой сплайн-функция проходит максимально близко к аппроксимируемым точкам в смысле наилучшего среднеквадратичного приближения.
Для этого используется функция SplineFit [data, type], которая возвращает сплайн функцию для данных data, используя сплайн-аппроксимацию типа type — по умолчанию это кубический сплайн Cube (другие типы — Bezier и CompositeBezier).
Рисунок 12.9 показывает пример сплайн- регрессии для обычной зависимости у(х), представленной пятью парами точек. На нем построены также графики аппроксимирующей функции и исходных точек.
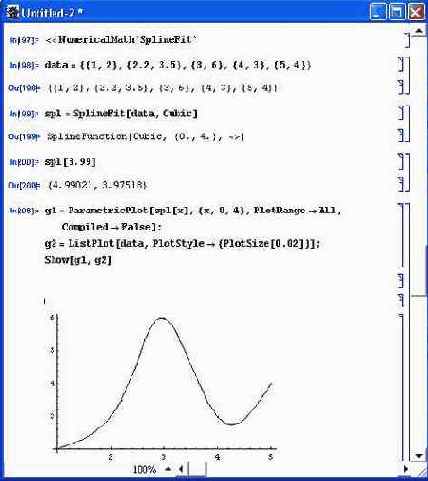
Рис. 12.9. Пример сплайн- регрессии для зависимости у(х), заданной списком координат своих узловых точек
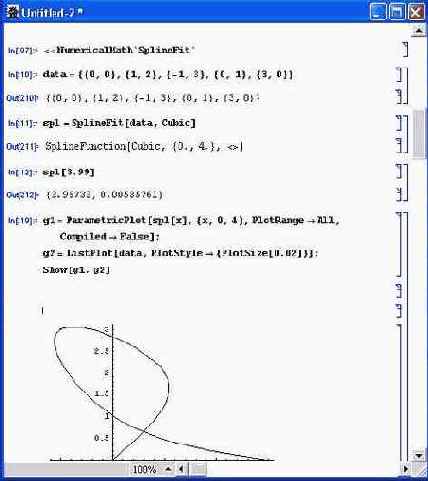
Рис. 12.10. Пример сплайн-интерполяции параметрически заданной функции
Специфика сплайн- регрессии по функции SplineFit заключается в преобразовании значений как xi, так и yi. Это позволяет представлять сплайнами в общем виде параметрически заданные функции, что поясняет рис. 12.10.
