Иллюстрированный самоучитель по Mathematica
Построение 3D-параметрических графиков — ParametricPlot3D
Трехмерные графики с параметрически заданными функциями, описывающими положение их точек, относятся к числу наиболее сложных, но в то же время весьма эффектных. В подпакете ParametricPlotSD определены функции, упрощающие подготовку таких графиков:
- ParametricPlot3D[{fx,fy,fz},{u,u0,ul,du},{v,c0,vl,dv}] — строит трехмерную поверхность, заданную параметрически функциями f x, f у и f z от переменных и и v с заданными диапазонами изменения и приращениями du и dv (рис. 14.60);
- PointParametricPlot3D[ { fx, f у, f z},{u,u0,ul,du}] — строит точками трехмерную поверхность, заданную параметрически функциями fx, f у и f z от одной переменной и с заданным диапазоном изменения и приращением du;
- PointParametricPlot3D[{fx,fy,fz},{u,u0,ul,du),{v,c0,vl,dv}] — строит точками трехмерную поверхность, заданную параметрически функциями fx, f у и f z от переменных и и v с заданными диапазонами изменения и приращениями du и dv.
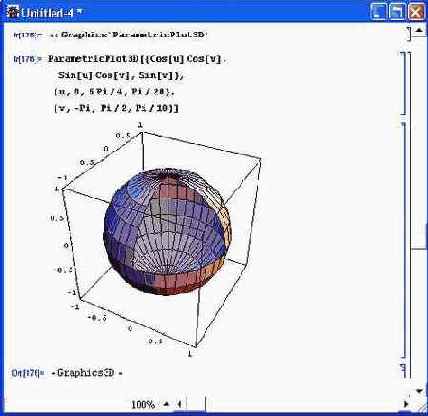
Рис. 14.60. Пример построения сферы с вырезом с помощью функции ParametricPlot3D
Обратите внимание на то, что выбором диапазона изменения углов можно получить вырез сферы. Окраска поверхности осуществляется автоматически.
На рис. 14.61 показан пример применения функции PointParametricPlotSD. Здесь сфера построена отдельными точками.
Для построения трехмерных поверхностей в сферической и цилиндрической системах координат служат следующие функции:
- SphericalPlot3D[r, {t, trnin, tmax}, {p,pmin,pmax} ] — построение графика в сферической системе координат;
- CylindricalPlot3D[z,{t,tmin,tmax},{p,pmin,pmax}] — построение графика в цилиндрической системе координат.
На рис. 14.62 показано построение усеченной сверху сферы с помощью функции SphericalPlot3D. Нетрудно заметить, что применение данной функции — самый простой способ построения сферы. Это естественно, поскольку система координат сферическая.
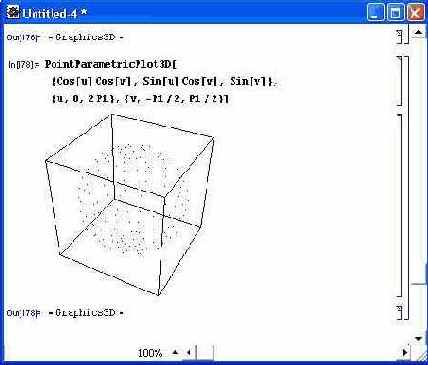
Риc. 14.61. Пример построения сферы точками
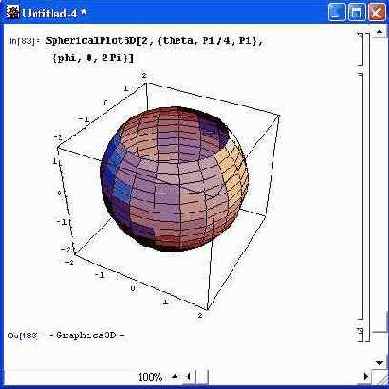
Рис. 14.62. Пример построения сферы с помощью функции SphericolPlot3D
Пример построения поверхности, напоминающей по виду «тарелку» спутниковой антенны, в цилиндрической системе координат дан на рис. 14.63.
С помощью опции Viewpoint можно изменять положение точки, с которой рассматривается фигура. Это существенно меняет ее вид (рис. 14.64).
Еще раз напоминаем, что интерфейс Mathematica предусматривает изменение точки просмотра уже построенной фигуры. При этом Mathematica 4 позволяет вращать фигуру мышью. Рекомендуется просмотреть список опций данных функций, позволяющих в широких пределах менять вид и стиль построения графиков.
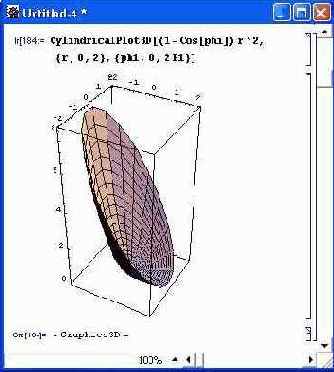
Рис. 14.63. Пример построения поверхности в цилиндрической системе координат
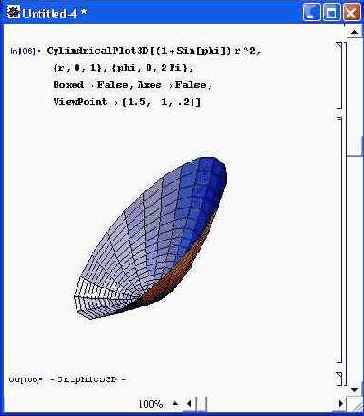
Рис. 14.64. Пример построения фигуры, видимой из заданной точки просмотра
