Построение графиков с множеством объектов — MultipleListPlot

В подпакете MultipleListPlot содержится расширенный вариант встроенной функции ListPlot:

MultipleListPlot [listl, Iist2,...] — строит множество графических объектов по данным списков. Списки могут быть представлены ординатами у, координатами точек {х,у), в виде {point, ErrorBar [ {negerr,poserr} ] } и т.д.

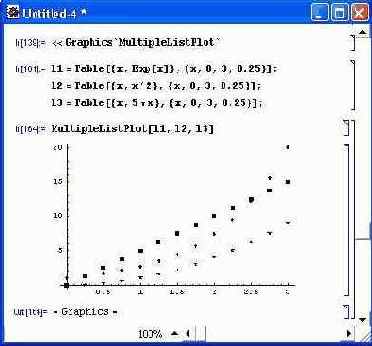
Рис. 14.52. Создание трех списков значений функций и их построение

Рисунок 14.52 иллюстрирует создание трех списков — 11, 12 и 13 — для трех функций и вывод их графиков в виде различных маленьких фигур.

Особое значение имеет опция Plot Joined. Если она используется в виде Plot-Joined->True, то это означает соединение точек на графиках отрезками линий разного стиля, выбираемого автоматически (рис. 14.53).

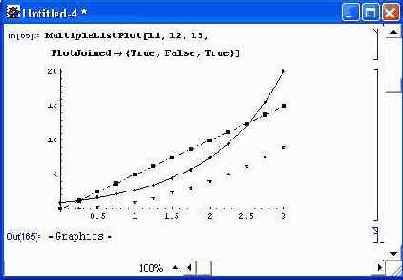
Рис. 14.53. Графики трех функций, построенные линиями, соединяющими их точки

Эта опция может быть представлена и со значением в виде списка. Например, ее применение в виде PlotJoined->{True, False, False} означает, что точки первой кривой соединяются линиями, тогда как точки второй и третьей кривых линиями не соединяются. Рисунок 14.54 поясняет этот способ построения графиков.

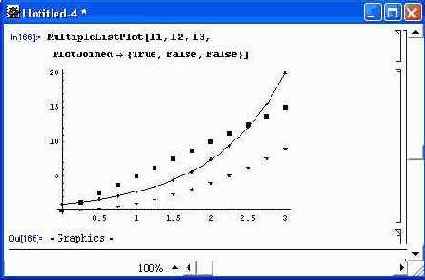
Рис. 14.54. Построение трех графиков, только у одного из которых точки соединены линиями

Функция MultipleListPlot может использовать в списках указания на построение точки с зоной погрешности (ErrorBar). Этот случай иллюстрирует рис. 14.55.

Более интересный случай построения точек с двумерными зонами погрешности в виде окружностей или эллипсов демонстрирует рис. 14.56.

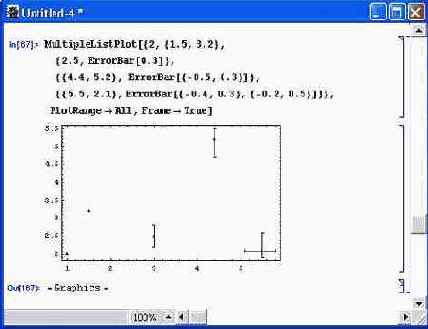
Рис. 14.55. Построение точек с одномерными зонами погрешности

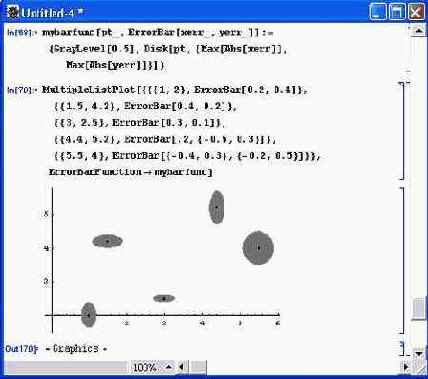
Рис. 14.56. Построение точек с двумерными зонами погрешности

Следующие функции служат для вывода символов в качестве точек:
PlotSymbol [type] — задает тип символа (возможные значения: Box, Diamond, Star или Triangle). Возможно применение опции_ Filled-> False;
PlotSymbol [type, size] — задает тип символа и его размер size;
MakeSymbol [primitives] — задает вывод символа, создаваемого графическим примитивом.

Рисунок 14.57 показывает построение точек с применением графических примитивов.
Этот путь позволяет обозначать точки графиков практически любыми фигурами.

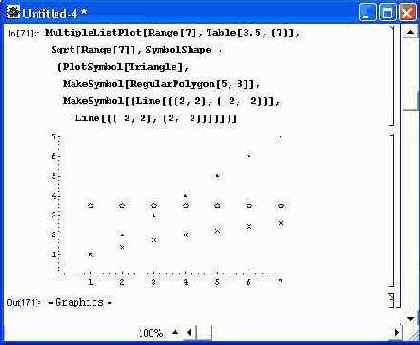
Рис. 14.57. Построение точек с применением графических примитивов

Для создания примитивов в виде правильных многоугольников (полигонов) используется директива RegularPolygon:

RegularPolygon [n] — правильный «-угольный полигон;
RegularPolygon [n, rad] — правильный и-угольный полигон с заданным радиусом описанной окружности rad;
RegularPolygon [n, rad, ctr] — то же с заданным центром ctr;
RegularPolygon [n, rad, ctr, tilt] — то же с углом поворота фигуры на tilt градусов;
RegularPolygon [n, rad, ctr, titl, k] — соединение линиями через k вершин.

Рисунок 14.58 показывает построение полигона — семиугольника с радиусом 3, центром в точке {0, 0}, углом поворота 20° и соединением через 3 вершины (попробуйте задать этот параметр другим целым числом и убедитесь, насколько меняется форма фигуры).

Директивы Dashing[ {Dot, Dash, LongDash,...} ] и AbsoluteDashing[ {Dot,...} ] служат для спецификации типа линий графиков. На рис. 14.59 представлены примеры такой спецификации и построения отрезков прямой линиями разных типов.

Применение функций подпакета MultipleListPlot наиболее ценно при визуализации математических расчетов, где преобладают графики тех типов, которые создаются этими функциями.

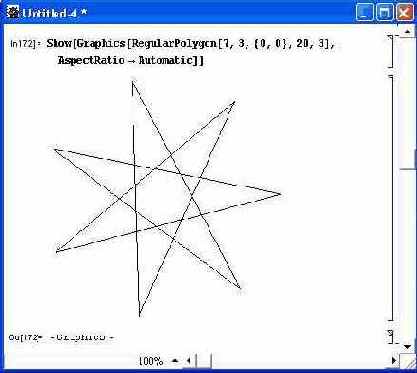
Рис. 14.58. Построение полигона

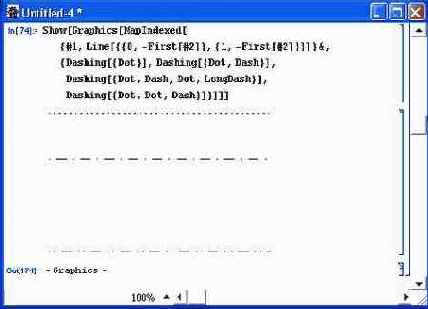
Рис. 14.59. Примеры построения отрезков прямых разными стилями

Содержание раздела