Иллюстрированный самоучитель по Mathematica
         

Построение полиэдров — Polyhedra



Подпакет Polyhedra служит для создания регулярных пространственных фигур — полиэдров. Они задаются как графические примитивы и выводятся функцией Show:

  • Show [Polyhedron [polyname] ] — строит полиэдр с именем polyname в центре графика;
  • Show[Polyhedron[polyname,{х,у,z},scale]] — строит полиэдр с именем polyname с центром в точке {х, у, z} и параметром масштаба scale.


Возможно задание следующих имен полиэдров: Tetrahedron, Cube, Octahedron, Dodecahedron, Icosahedron, Hexahedron, GreatDodecahedron, Small-StellatedDodecahedron, GreatStellatedDodecahedron и Greatlcosa-hedron. Пример построения полиэдра Icosahedron показан на рис. 14.74.

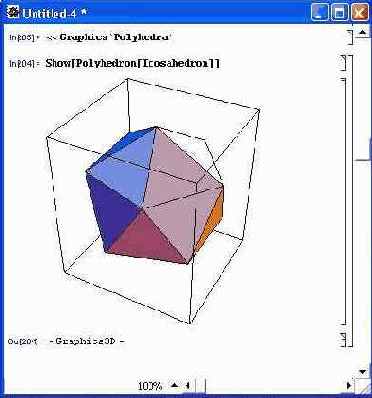
Рис. 14.74. Построение полиэдра Icosahedron

Возможность вывода с помощью функции Show двух полиэдров иллюстрирует рис. 14.75.

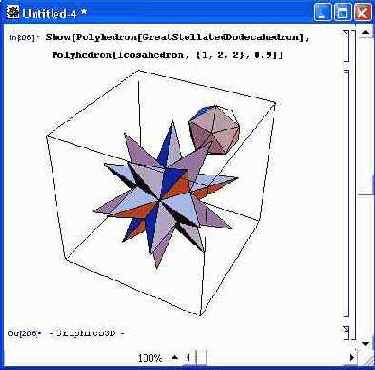
Рис. 14.75. Вывод функцией Show двух полиэдров

Для вывода полиэдров служит также ряд описанных ниже функций. Так, для построения звездчатых форм полиэдров предназначена функция Stellate:

  • Show [Stellate [Polyhedron [polyname] ] — построение звездчатых форм полиэдров;
  • Show[Stellate[Polyhedron[polyname], ratio] — построение звездчатых форм полиэдров с заданным отношением радиусов описанной и вписанной сфер ratio.

Рисунок 14.76 показывает построение звездообразного (или игольчатого) полиэдра. Представленная фигура напоминает некоторых морских животных — ежей и звезд.

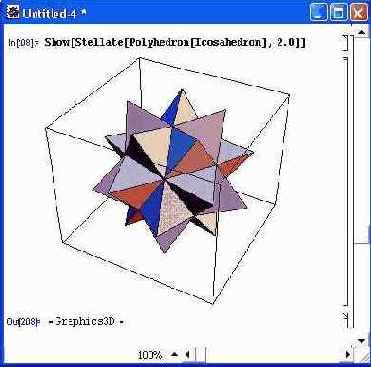
Рис. 14.76. Построение звездчатой формы полиэдра

Полиэдры, применяемые в геодезии, можно получить с помощью следующей функции:

  • Show [Geodesate [Polyhedron [polyname], n] — построение полиэдра с вершинами, лежащими на сфере, представляющего собой результат я-кратно-го разбиения на треугольники граней полиэдра polyname;
  • Show [Geodesate [Polyhedron [polyname] , n, {x, y, z}, radius] —построение полиэдра с вершинами, лежащими на сфере с заданным положением центра {x,y,z} и радиусом radius, представляющего собой результат п-кратного разбиения на треугольники граней полиэдра polyname.

Рисунок 14.77 показывает применение этой функции.


Для построения усеченных полиэдров предназначены следующие функции:

  • Show [Truncate [Polyhedron [polyname] ] ] — построение усеченных полиэдров;
  • Show [Truncate [Polyhedron [polyname], ratio] — построение усеченных полиэдров с заданным коэффициентом усечения ratio (от 0 до 0.5);
  • Show[OpenTruncate[Polyhedron[polyname]]] — построение полиэдров с открытым усечением;
  • Show[OpenTruncate[Polyhedron[polyname], ratio] — построение полиэдров с открытым усечением и заданным коэффициентом усечения ratio (от 0 до 0.5).


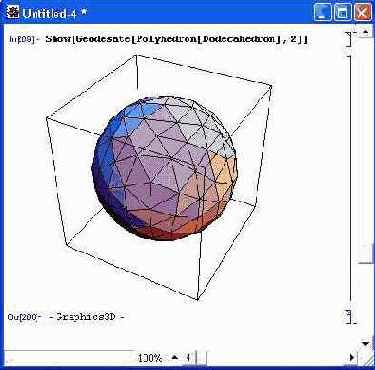
Рис. 14.77. Построение полиэдра в виде сферы

Рисунок 14.78 показывает построение усеченного полиэдра Усечение сделано так, будто полиэдр заполнен материалом. Поэтому усеченные области выглядят как дополнительные грани. Параметр ratio, задающий степень усечения, может иметь значения от 0 до 0.5 (в ином случае выводятся сообщения об ошибке в задании параметра).



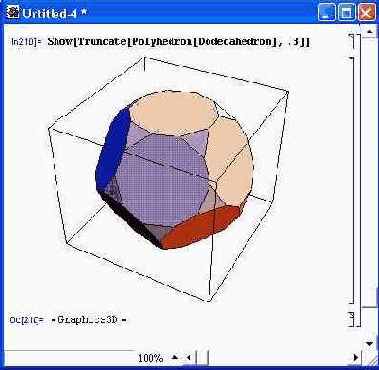
Рис. 14.78. Построение усеченного полиэдра

Усечение может быть открытым — такой вариант реализуется функцией со словом Open в имени. В этом случае фигура выглядит так, будто она склеена из тонкого картона (рис. 14.79). При этом в местах усечения фигура прозрачна.



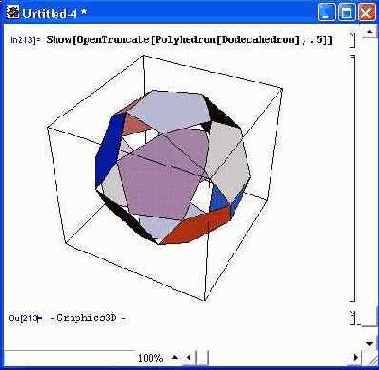
Рис. 14.79. Построение усеченного полиэдра с открытыми местами усечения

В заключение этого раздела отметим следующие функции:

  • First [Polyhedron [polyname] ] — возвращает список полигонов для указанного полиэдра;
  • Vertices [polyname] — возвращает список координат вершин полиэдра;
  • Faces [polyname] — возвращает список вершин, ассоциированных с каждой гранью.
Они ничего не строят, а лишь возвращают специфические параметры полиэдров. Примеры применения этих функций представлены ниже:

First[ Polyhedron[ Octahedron ]]

{Polygon[{{0, 0, 1.41421}, {1.41421, 0, 0}, {0, 1.41421, 0}}],

Polygon[{{0, 0, 1.41421}, {0, 1.41421, 0}, {-1.41421, 0, 0}}],

Polygon[{{0, 0, 1.41421}, {-1.41421, 0, 0}, {0, -1.41421, 0}}],

Polygon[{{0, 0, 1.41421}, {0, -1.41421, 0}, {1.41421, 0, 0}}],

Polygon[{{1.41421, 0, 0}, {0, -1.41421, 0}, {0, 0, -1.41421}}],

Polygon[ {{1.41421, 0, 0}, {0, 0, -1.41421}, {0, 1.41421, 0}}],

Polygon[{{0, 0, -1.41421}, {0, -1.41421, 0}, {-1.41421, 0, 0}}],

Polygon[{{0, 1.41421, 0}, {0, 0, -1.41421}, {-1.41421, 0, 0}}]}

Vertices[ Octahedron ]

{{0, 0, 1.41421}, {1.41421, 0, 0},

{0, 1.41421, 0}, {0, 0, -1.41421},

{-1.41421, 0, 0}, {0, -1.41421, 0}}

Faces[ Octahedron ]

{{1, 2, 3}, {1, 3, 5}, {1, 5, 6},

{1, 6, 2}, {2, б, 4}, {2, 4, 3}, {4, б, 5}, {3,4,5}}

Приведенные выше функции можно использовать на занятиях по стереометрии, где полученные с их помощью фигуры могут прекрасно иллюстрировать теоретические положения курса.



Содержание раздела