Иллюстрированный самоучитель по Mathematica
Представление полей на плоскости — PlotField
В подпакете PlotField имеются функции, позволяющие строить стрелками графики полей:
- PlotVectorField[ {fx, f у}, {x, xmin, xmax), {y, ymin, ymax} ] —строит плоскость из векторов (стрелок), ограниченную пределами изменения х и у;
- PlotGradientField[f,{x,xmin,xmax},{у,ymin,ymax}] — строит плоскость из векторов (стрелок) градиента функции f, ограниченную пределами изменения х и у;
- PlotHamiltonianField[f,{x,xmin,xmax},{у,ymin,ymax}] — строит плоскость из векторов (стрелок) гамильтониана функции f, ограниченную пределами изменения х и у;
- PlotPolyaField[f, {х,xmin,xmax}, {у, ymin, ymax} ] — представляет график комплексной функции f(x, у).
Рисунок 14.65 показывает применение функции PlotVectorField для построения векторного поля согласно параметрически заданной на плоскости функции.
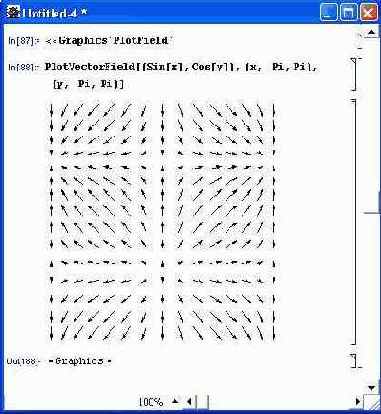
Риc. 14.65. График векторного поля на плоскости
Еще один пример (рис. 14.66), иллюстрирует построение градиента поля с помощью функции PlotGradientField. Применение функции PlotHamiltonianField демонстрирует рис. 14.67.
Указанные функции имеют множество опций. Отметим основные из них (в качестве значений приведены значения по умолчанию):
- ScaleFactor->Automatic — устанавливает размер векторов (стрелок);
- ScaleFunction->None — устанавливает функцию, вычисляющую размер стрелок;
- MaxArrowLenght->None — устанавливает ограничение длины стрелок;
- ColorFunction->None — задает функцию цвета;
- PlotPoints->15 — задает число точек по координатам для построения стрелок.
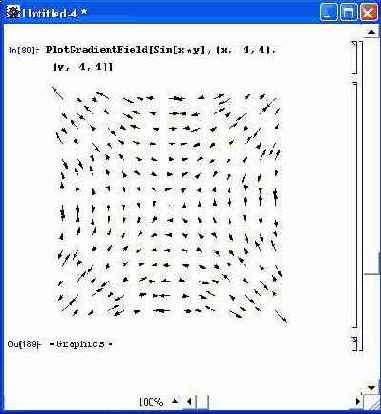
Рис. 14.66. График градиента поля
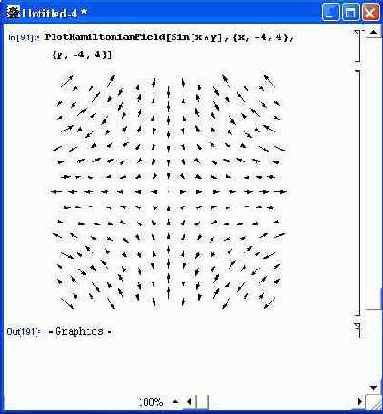
Риc. 14.67. Пример применения функции PlotHamiltonianField
Пример построения сложного графика с применением шестнадцати узловых точек по каждому направлению и использованием опции ScaleFunction показан на рис. 14.68.
Работу функции PlotPolyaField поясняет рис. 14.69. Обратите внимание на то, что функция в данном случае комплексная.
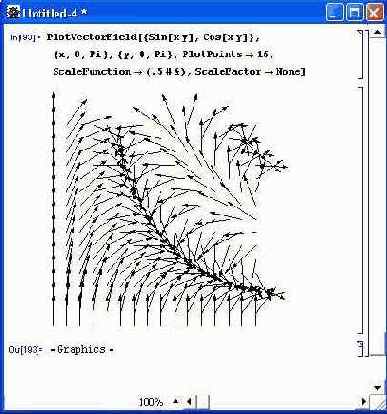
Рис. 14.68. Пример графика поля с применением нескольких опций
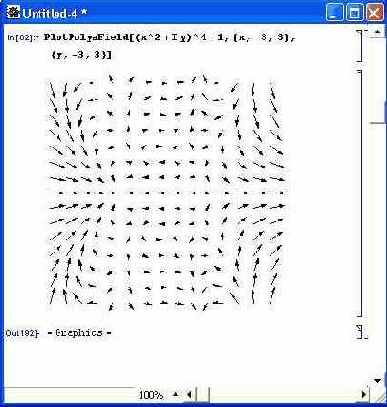
Рис. 14.69. Пример графика поля для комплексной функции
Применение опций позволяет строить самые разнообразные графики различных полей — тепловых, гравитационных, электрических и др.
В подпакете PlotField есть еще одна функция, представляемая в двух формах:
- ListPlotVectorField [ {{vect 11, vect12,...},{vect21, vect22,...},...} ] — строит график векторного поля прямоугольного массива векторов vect xy ;
- ListPlotVectorField [{{pt1, vect1,...}, (pt2,vect2,...},...}] —строит график векторного поля по списку векторов vect xy , расположенных в точках pti.
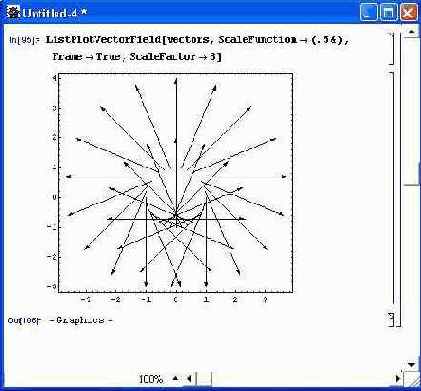
Рис. 14.70. Пример построения графика векторного поля с помощью функции ListPlotVectorField
Приведенных примеров вполне достаточно, чтобы судить о возможностях подпа-кета PlotField. В справочной базе данных можно найти другие примеры построения графиков векторных полей.
