Создание графических форм — Shapes

Нередко желательно придать трехмерным объектам определенную форму, например кольца или бублика. Некоторые возможности для этого дают функции под-пакета Shapes. Основной из них является функция Show [Graphics3D [shape] ], которая производит отображение формы со спецификацией shape.

С ней могут использоваться графические примитивы:

Cone [r, h, n] — конус с основанием радиуса r и высотой h на основе n-сто-роннего полигона;
Cylinder [r, h, n] — цилиндр радиуса r и высотой h на основе и-стороннего полигона;
Torus[rl,r2,n,m] — объемное кольцо с внешним и внутренним радиусами rl и г 2 и числом сторон каркаса n и m;
Sphere [r, n,m] — сфера радиуса г, составленная из многоугольников с параметрами n и m и числом сторон п(т - 2) + 2;
MoebiusStrip [rl, r2, n] — кольцо Мебиуса с радиусами rl и r2, построенное на основе полигона с 2n сторонами;
Helix[r,h,m,n] — плоская спираль радиусом г и высотой h c m витками на основе поверхности, разбитой на nxm четырехугольников;
DoubleHelix[r,h,m,n] — плоская двойная спираль радиусом r и высотой h с m витками на основе поверхности, разбитой на nxm четырехугольников.

Возможно указание фигур без параметров. Это означает, что они выбираются по умолчанию следующими:

Соnе[1, 1, 20]

Cylinder[1, 1, 20]

Helix[l, 0.5, 2, 20]

DoubleHelix[l, 0.5, 2, 20]

MoebiusStrip[1, 0.5, 20]

Sphere[l, 20, 15]

Torus[l, 0.5, 20, 10]

На рис. 14.80 показан пример построения фигуры DoubleHelix без указания ее параметров с помощью функций Show и GraphicsSD.

Рисунок 14.81 показывает построение другой фигуры — кольца Мебиуса с указанием параметров фигуры. Обратите внимание на то, что в обоих случаях автоматически обеспечивается функциональная окраска фигур, облегчающая их восприятие.

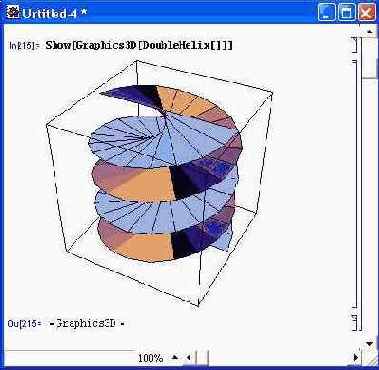
Рис. 14.80. Пример построения фигуры без указания параметров

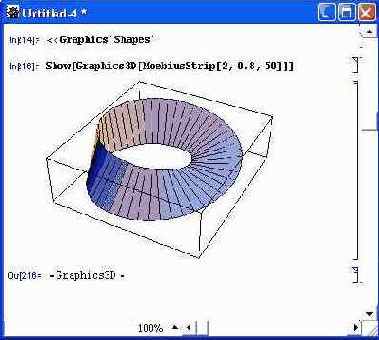
Рис. 14.81. Построение кольца Мебиуса

Для преобразования графических объектов в подпакете Shapes имеются следующие функции:

RotateShape [g,phi, theta,psi] — поворот графического объекта на углы phi, theta и psi;
TranslateShape [g, {х, у, z} ] — сдвиг графического объекта на расстояния {х,у, z};
Af fineShape [g, {scalel, svale2, scaleS} ] — умножение всех координат объекта g на указанные множители.

Рисунок 14.82 иллюстрирует осуществление вращения для кольца Мебиуса.
Эффект вращения хорошо заметен, если сравнить положения фигуры на рис. 14.81 и 14.82.

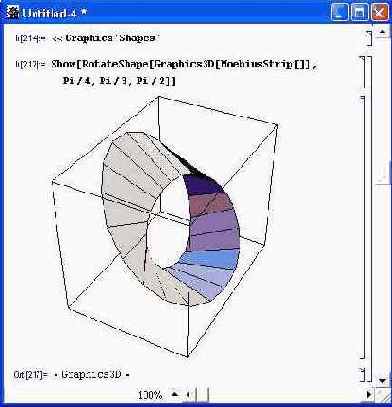
Рис. 14.82. Кольцо Мебиуса после поворота

Функции Show и Graphics3D позволяют строить трехмерные фигуры, которые пересекаются в пространстве. Пример такого построения приведен на рис. 14.83. Нетрудно заметить, что линии пересечения строятся с точностью до одной ячейки — полигона. Поэтому для получения качественных фигур надо увеличивать число полигонов, из которых фигуры синтезируются. Это, однако, увеличивает время построения фигур — оно становится заметным даже при работе на современных компьютерах с процессорами Pentium II и Pentium III.

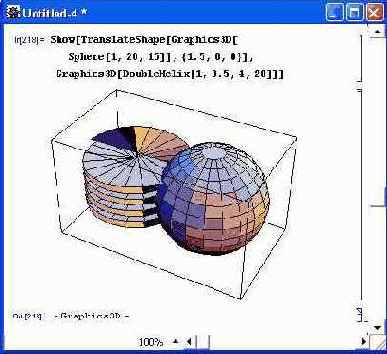
Рис. 14.83. Фигуры, пересекающиеся в пространстве

В заключение этого раздела отметим, что функция WireFrame [g] дает «каркас» графического объекта, то есть делает все его грани прозрачными. Применение этой функции иллюстрирует пример, показанный на рис. 14.84.

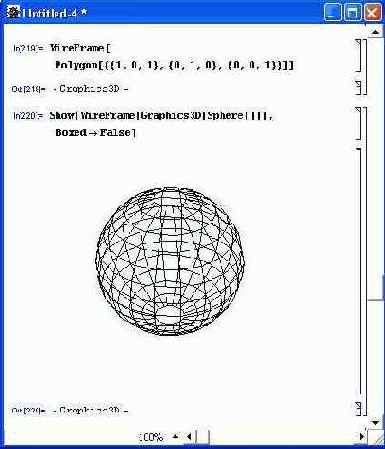
Рис. 14.84. Пример применения функции WireFrame для построения каркаса сферы

Содержание раздела