Иллюстрированный самоучитель по Mathematica
Численные данные
Двоичные числа, биты и байты
Минимальной единицей информации в компьютерной технике является двоичная единица — бит. Она имеет представление в виде 0 или 1, удобное для реализации простейшими электронными схемами с двумя состояниями электрического равновесия (например, триггерами или иными ячейками памяти). Многоразрядные двоичные числа представляют собой набор цифр 0 и 1, например, 100110 или 111001. Каждый старший разряд относительно предыдущего имеет весовой коэффициент, равный 2.
Именно с битами работает микропроцессор на нижнем уровне операций. Однако бит — слишком мелкая единица, не очень удобная в обращении. К тому же мы привыкли к куда более удобным и наглядным для нас элементам информации, таким как буквы, цифры, знаки арифметических операций, спецзнаки и символы псевдографики. В принципе, набор этих знаков, минимально необходимый для представления обычной текстовой и цифровой информации, содержит до 2 8 = 256 элементов. Каждый из них в компьютере представляется кодом от 0 до 255. Для задания таких кодов достаточно 8 бит (2^8=256), которые и образуют наиболее распространенную единицу представления информации — байт. 1024 байта образуют килобайт (Кбайт), 1024 Кбайт дают 1 Мбайт (мегабайт) и т. д.
Широко применяется общеизвестный стандарт кодирования текстовой информации ASCII (American Standard Code for Information Interchange).
Десятичные числа
К наиболее известным типам данных в математике относятся привычные нам десятичные числа (DECIMAL). Каждый разряд таких чисел имеет представление, заданное одной из арабских цифр — 0, 1, 2,..., 9. Весовой коэффициент старшего разряда относительно предшествующего равен 10. Количество цифр, представляющих число, может быть, в принципе, любым. Десятичные числа относятся к следующим основным типам.
|
Обозначение |
Тип чисел |
Примеры задания |
|
|
Integer |
Целочисленные |
123 |
-345 |
|
Rational |
Рациональные |
123/567 |
-23/67 |
|
Real |
Вещественные |
123. |
-123.45610 ^ 6 |
|
Complex |
Комплексные |
-3.5 + 0. |
56 I |
Десятичные числа наиболее распространены в научно-технических расчетах.
Целые числа
Целочисленные данные (Integer) — это целые числа, например 1, 2 или 123, которые представляются системой без погрешности и ограничения разрядности. Более того, арифметические операции над целыми числами система выполняет также без погрешностей и без ограничения числа цифр (рис. 3.1).
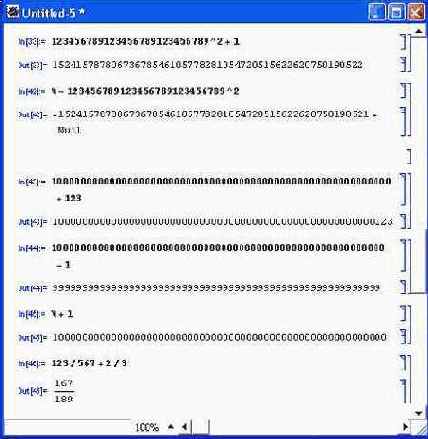
Рис. 3.1. Операции с целыми числами
Количество цифр, представляющих большое целое число, ограничено лишь его значением, но не какими-либо фиксированными форматами. Рациональные данные задаются отношением целых чисел, например 123/567, и также представляют результат точно. Поэтому система при символьных и численных расчетах всегда старается выдать результат в виде целых или рациональных чисел, там где это возможно:
1000000/3000000
1/3
(124-1)/(455+1)
41/152
Фактически целые числа произвольной разрядности в системах символьной математики представляются списками отдельных цифр. Особая организация списков повышает компактность представления больших целых чисел. Характерным примером работы с целыми числами большой разрядности является вычисление факториала n!=1*2*3*. . . *n. Примеры его вычисления уже приводились (см. рис. 1.16).
Числа с произвольным основанием
Для вычисления чисел с произвольным основанием используется конструкция
Основание^^Число
Число должно быть записано по правилам записи чисел с соответствующим основанием. Если основание больше 10, для обозначения значений чисел используются буквы от а до z. Наиболее известными из чисел с основанием системы счисления, превышающим 10, являются шестнадцатеричные числа (HEX — от слова hexagonal). Разряды таких чисел могут иметь следующие значения:
HEX 0123456789abCdef
DECIMAL 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Каждый более старший разряд имеет весовой коэффициент относительно предыдущего разряда, равный 16.
Примеры задания шестнадцатеричного и двоичного чисел:
16^^123abcde
305839326
2^^1010111
87
Для представления чисел с произвольным основанием n (до 32) используется функция BaseForm[expr, n], которая возвращает выражение ехрг в форме числа с основанием n, которое указывается как подстрочный индекс.
Примеры использования функции BaseForm:
BaseForm[87,2]
10101112
BaseForm[305839326,16]
123abcde16
В дальнейшем мы будем использовать только десятичные числа.
Вещественные числа
Численные данные могут быть представлены также десятичными вещественными числами, которые могут иметь различную форму, например 123.456, 1.23456 10^2,12345.6 10^-2 и т. д. В общем случае они содержат мантиссу с целой и дробной частями и порядок, вводимый как степень числа 10. Как правило, вещественные числа в системах символьной математики могут иметь мантиссу с любым, но конечным числом знаков. Пробел между мантиссой и порядком эквивалентен знаку умножения *:
23.456*10^100
2.345бх10^101
10^-100
1/
100000000000000000000000000000
0000000000000000000000000000
0000000000000000000000000000000000000000000
10.^-100
1.x 10^-100
Как принято в большинстве языков программирования, целая часть мантиссы отделяется от дробной части точкой, а не запятой.
Mathematica производит операции с числами изначально как с целыми. Однако установка значка разделительной точки означает, что число должно рассматриваться как вещественное. Например, 1 — целое число, но 1. — уже вещественное число. Для представления выражения ехрг в форме вещественного числа используется функция N [ехрг] или N [ехрг, число_цифр_результата].
Примеры:
1/3
1/3
1./3 .
0.333333
N[1/3]
0.333333
N[2*Pi,50]
6.283185307179586476925286766559005768394338
Вещественные числа всегда имеют некоторую погрешность представления результатов из-за неизбежного округления и существования так называемого машинного нуля — наименьшего числа, которое воспринимается как нуль. В терминах системы Mathematica говорят о приближении числовых данных как об их аппроксимации, хотя в отечественной литературе под аппроксимацией чаще подразумевают описание некоторой зависимости между данными достаточно приближенной аналитической зависимостью.
Mathematica имеет две системные переменные, позволяющие вывести максимально и минимально возможные значения чисел, с которыми оперирует система:
$MaxMachineNumber
1.79769х10^308
$MinMachineNumber
2.22507х 10^-308
Обратите внимание на то, что функция N [ехрr, m] позволяет получить число с практическим любым числом цифр результата m. Разработчики последней версии Mathematica 4 утверждают, что это верно при количестве цифр результата до одного миллиона, что с лихвой удовлетворяет требованиям подавляющего большинства расчетов и вычислений.
Функции IntegerPart [x] и FractionalPart [x] обеспечивают возврат целой и дробной частей вещественного числа х:
N[Pi]
3.14159
IntegerPart[Pi]
3
FractionalPart[Pi]
-3.+ Л
N[FractionalPart[Pi]]
0.141593
Еще одна функция RealDigits [x] возвращает список реальных цифр результата и число цифр целой части х:
RealDigits[N[2*Pi]]
{{6, 2, 8, 3, 1, 8, 5, 3, 0, 7, 1, 7, 9, 5, 8, 6}, 1}
Есть и множество других функций для работы с вещественными числами. Они будут рассмотрены в дальнейшем. В Mathematica 4 функция RealDigits имеет расширенные формы, например RealDigits [x, b, len, n]. Для получения цифр мантиссы введены функции MantissaExponent [x] и MantissaExpo-nent[x,b].
Комплексные числа
Многие математические операции базируются на понятии комплексных чисел. Они задаются в форме
z=Re(z)+I*Im(z)
или
z=Re(z)+i Im (z)
где знак I (i) — мнимая единица (квадратный корень из -1), Re (z) — действительная часть комплексного числа, a Im (z) — мнимая часть комплексного числа. Пример задания комплексного числа:
2 + I3
или
2 + 3*I
Мнимая часть задается умножением ее значения на символ мнимой единицы I. При этом знак умножения * можно указывать явно или заменить его пробелом — в последнем случае комплексное число выглядит более естественным. Функции Re [ z ] и Im [ z ] выделяют, соответственно, действительную и мнимую части комплексного числа z. Это иллюстрируют следующие примеры:
Re[3+2*1]
3
Im[3+2 I]
2
Большинство операторов и функций системы Mathematica работают с комплексными числами. Разумеется, это расширяет сферу применения системы и позволяет решать с ее помощью различные специальные задачи — например, относящиеся к теории функций комплексного аргумента.Комплексные числа широко используются в практике электро- и радиотехнических расчетов на переменном токе.
