Иллюстрированный самоучитель по Mathematica
Преобразования Фурье
Основные понятия о спектральном анализе и синтезе
Спектральный подход (метод) лежит в основе целых направлений науки и техники. Достаточно отметить, что он плодотворно используется в технике электро- и радиосвязи, где разделение частот модулированных сигналов базируется на различии их спектров. Спектральный подход также широко используется для создания аналоговых и цифровых фильтров и для оценивания искажений сигналов в ходе их преобразования, например усиления реальными усилителями.
Схема применения спектрального подхода достаточно проста. Сигнал вначале представляется совокупностью гармонических составляющих — гармоник ~ в виде тригонометрического ряда Фурье. Для точного представления сигнала требуется бесконечное число гармоник, но на практике оно всегда ограничено. Такое ограничение порождает волнообразный характер изменения сигнала и появление выбросов, что известно под названием эффекта Гиббса.
Получение сигнала в виде суммы гармонических составляющих получило название спектрального анализа. Суммирование гармоник сигнала и его приближенное представление во временной области называется гармоническим синтезом сигнала.
Итак, спектральный подход заключается в следующем. Вначале получают достаточно представительный (с большим числом гармоник) спектр заданного сигнала. Довольно часто используют тестовые сигналы в виде прямоугольных, треугольных, пилообразных и других импульсов. Для моделирования таких сигналов можно использовать различные функции, например, Sign [Sin [t] ] позволяет получить симметричные прямоугольные импульсы (меандр), а Abs [Sin [t] ] моделирует результат двухполупериодного выпрямления синусоидального напряжения. Для получения разрывных сигналов можно использовать функции с условиями сравнения, например функцию If (на рис. 5.4 даны примеры имитации с помощью этой функции импульсов прямоугольной и пилообразной формы).
Для многих частных видов сигналов (а к ним относится большинство тестовых сигналов) разложения в ряд Фурье хорошо известны и приводятся в любом математическом справочнике (иногда в несколько разных формах).
Это позволяет сразу получить нужное число гармоник сигнала и, что особенно важно, проверить, насколько адекватно синтезируемый сигнал описывает реальный сигнал.
На рис. 5.5 показан пример прямого синтеза разнополярных коротких прямоугольных импульсов. Используется известное разложение их в ряд, причем графики построены для 5 и 20 гармоник. Нетрудно заметить, что даже при двадцати гармониках представление такого сигнала гармоническим рядом не очень точно — отчетливо наблюдаются колебания и выбросы, то есть эффект Гиббса.
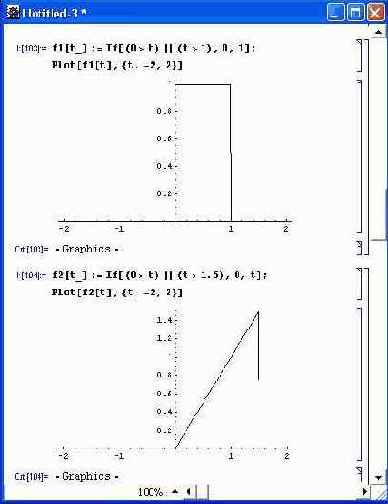
Рис. 5.4. Имитация импульсов прямоугольной и пилообразной формы с помощью функции If
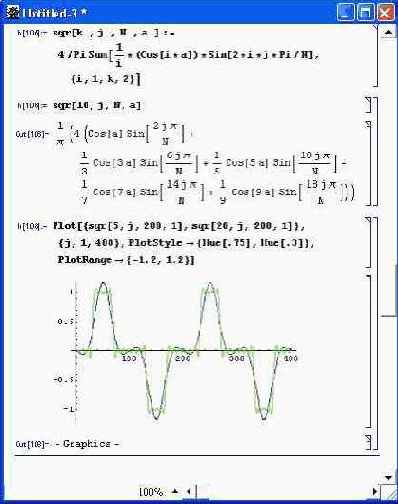
Рис. 5.5. Гармонический синтез коротких разнополярных прямоугольных импульсов
Еще один подобный пример — синтез разнополярных треугольных импульсов — представлен на рис. 5.6. Здесь также используется известное выражение для ряда
Фурье. Графики построены для 3 и 20 гармоник. Нетрудно заметить, что гармонический синтез для этого сигнала дает гораздо лучшие результаты — даже три гармоники неплохо воспроизводят сигнал. Это связано с тем, что данный сигнал не имеет разрывов — для него характерны лишь точки резких перегибов временной зависимости.
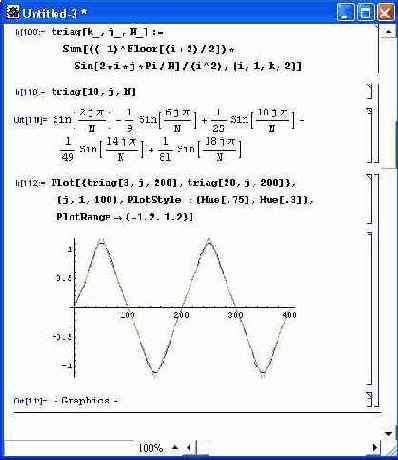
Рис. 5.6. Гармонический синтез симметричных треугольных импульсов
В целом надо отметить, что чем плавнее временная зависимость сигнала, тем меньше проявляются отмеченные выше искажения и слабее заметен эффект Гиббса.
Итак, в результате гармонического анализа сигнала (или его прямого гармонического синтеза) сигнал получается в виде совокупности гармонических сигналов — гармоник. В общем случае каждая гармоника имеет свою амплитуду и фазу, и для их получения в общем случае можно использовать прямое преобразование Фурье (см. ниже).
Полученный спектр сигнала можно подвергать различным преобразованиям, например частотной фильтрации. Полученный после этого измененный спектр гармоник используется (путем гармонического синтеза) для воссоздания искаженного (например, после фильтрации) сигнала.
Простота спектрального подхода обманчива, поскольку он требует довольно громоздких вычислений.Для быстрого их выполнения были созданы различные ускоренные методы спектрального анализа и синтеза — например, метод быстрого преобразования Фурье (БПФ). Но лишь с появлением СКМ класса Mathematica (и ей подобных) спектральный подход превращается в «рабочую лошадку», обеспечивая наглядное и достаточно быстрое решение задач спектрального анализа и синтеза.
