Иллюстрированный самоучитель по Mathematica
Функции Бесселя
Функции Бесселя, являющиеся решениями линейных дифференциальных уравнений вида z 2 y" + zy'+ (z 2 - п 2 )у = 0, широко используются в анализе и моделировании волновых процессов. В системе Mathematica к этому классу относятся следующие функции:
- Bessell[n, z] — модифицированная функция Бесселя первого рода I(n, z);
- BesselJ[n, z] — функция Бесселя первого рода J(и, z);
- BesselK[n, z] — модифицированная функция Бесселя второго рода К(п, z);
- BesselY[n, z] — функция Бесселя второго рода Y(n, z).
Соотношения между этими функциями хорошо известны. Следующие примеры показывают вычисление функций Бесселя.
| Ввод (In) | Вывод (Out) |
| Bessell[0,l.] | 1.26607 |
| Bessell[3,l.] | 0.0221684 |
| Bessell[l,2.+3.*I] | -1.26098 + 0.780149 I |
| Bessell[2,2.+3.*I] | 1.25767 + 2.31877 I |
| BesselK[2,2.+3.*I] | -0.0915555 + 0.0798916 I |
| BesselY[2,2.+3.*I] | -2.3443 + 1.27581 I |
| BesselY[2,2.+3.*I] | |
| N[BesselJ[l,0.5]] | 0.242268 |
| N[BesselJ[l, 2+1*3]] | 3.78068- 0.812781 I |
Приведем также пример на вычисление производной от функции Бесселя:
D[BesselJ[l, x], (х, 2}]
1/2 (-BesselJ[l, x] +
1/2 (-BesselJ[l, x] +BesselJ[3, x]) )
Нетрудно заметить, что результат в данном случае также представлен через функции Бесселя.
В другом примере — вычислении интеграла от функции Бесселя — результат выражается через гипергеометрическую функцию:
Integrate[BesselJ[2,x],x]
1/24 x3 HypergeometricPFQ [ { 2/3 }, { 5/2,3}, -x2/4]
На рис. 6.7 показаны графики функций Бесселя Bessell и BesselJ первых четырех порядков.
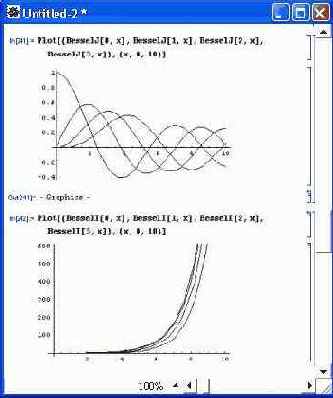
Рис. 6.7. Графики функций Бесселя Bessell (сверху) и Bessell (снизу) первых четырех порядков
Графики других функций Бесселя вы можете получить самостоятельно. Они представляют меньший интерес, чем графики, приведенные на рис. 6.7.
 |
 |
 |
