Иллюстрированный самоучитель по Mathematica
Примитивы двумерной графики
Примитивами двумерной графики называют дополнительные указания, вводимые в функцию Graphics [primitives, options], которая позволяет выводить различные примитивные фигуры без задания математических выражений, описывающих эти фигуры. Примитивы могут выполнять и иные действия. Они заметно увеличивают число типов графиков, которые способна строить система Mathematica. Имеются примитивы для построения окружностей, эллипсов, кругов, овалов, линий и полигонов, прямоугольников и текстов. Полное описание примитивов дано в разделе приложения, посвященном данному уроку. Примитивы задаются подобно графическим функциям, например, Circle[{x, у}, r] строит окружность с радиусом г и центром в точке {х, у}.
Рисунок 8.10 показывает применение функции Graphics для построения одновременно трех графических объектов: отрезка прямой, заданного координатами его концевых точек, окружности с центром (0, 0) и радиусом 0.8 и текстовой надписи «Привет!». Каждый объект задан своим примитивом. Из-за искажения масштаба дисплеем компьютера окружность выглядит как эллипс.
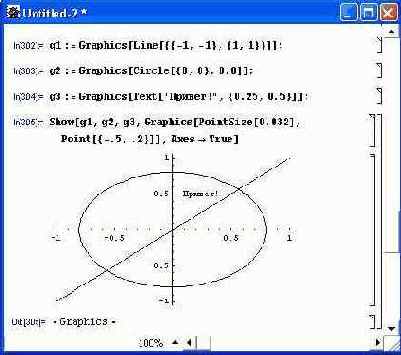
Рис. 8.10. Построение трех графических объектов с помощью примитивов двумерной графики
На другом рисунке (рис. 8.11) представлено построение пятиугольника, заданного координатами его вершин.
Приведенные примеры поясняют технику применения графических примитивов. Но они, разумеется, не исчерпывают всех возможностей этого метода построения геометрических фигур и объектов. Все указанные примитивы используются при построении как двумерных, так и трехмерных графиков.
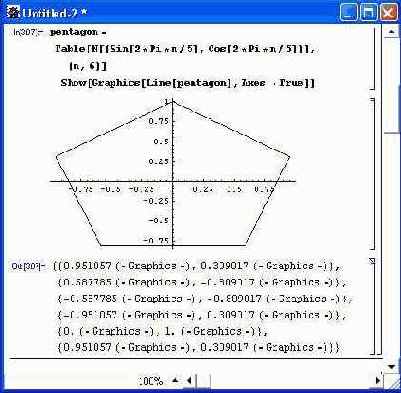
Рис. 8.11. Построение пятиугольника
Графики функций, заданных в параметрической форме
Построение графиков в полярной системе координат возможно двумя способами. Первый способ основан на использовании обычной декартовой системы координат. Координаты каждой точки при этом задаются в параметрическом виде: x = f
x
(t) и у
=
f
y
(t), где независимая переменная t меняется от минимального значения £
min
до максимального t
mах
с шагом dt.
Особенно удобно применение таких функций для построения замкнутых линий, таких как окружности, эллипсы, циклоиды и т. д. Например, окружность радиусом R может быть задана в следующей параметрической форме: х = R cos(t) и у = R sin(t), если t меняется от 0 до 2п. В общем случае радиус также может быть функцией параметра t.
Для построения параметрически заданных функций используются следующие графические средства:
- ParametricPlot [ {fx, fy}, {t, tmin, tmax} ]—строит параметрический график с координатами f х и f у (соответствующими х и у), получаемыми как функции от t;
- ParametricPlot [{{fx, fy}, {gx, gy},...}, {t, tmin, tmax}] —строит графики нескольких параметрических кривых.
Рисунок 8.12 показывает построение параметрически заданной фигуры Лиссажу. Она задается функциями синуса и косинуса с постоянным параметром R и аргументами, кратными t. Эти фигуры наблюдаются на экране электронного осциллографа, когда на его входы X и Y подаются синусоидальные сигналы с кратными частотами.
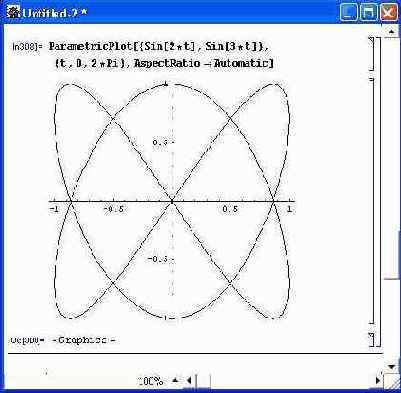
Рис. 8.12. Построение фигуры Лиссажу
На одном графике можно строить две и более фигур с заданными параметрически уравнениями. На рис. 8.13 показан пример такого построения — строятся две фигуры Лиссажу, причем одна из них является окружностью. Больше двух фигур строить нерационально, так как на черно-белом графике их трудно различить.
Теперь рассмотрим второй способ построения графиков в полярной системе координат (рис. 8.14). Здесь каждая точка является концом радиус-вектора R(t), причем угол t меняется от 0 до 2я. На рис. 8.14 функция R(t) задана как функция пользователя R[t_] с использованием образца t_ для задания локальной переменной t в теле функции.
Изменение параметра R позволяет заметно увеличить число отображаемых функций — фактически, их бесконечно много. Помимо описанной фигуры на рис. 8.14 дополнительно построена линия окружности единичного радиуса.
Чтобы она имела правильные пропорции на экране, задана опция AspectRatio->l.
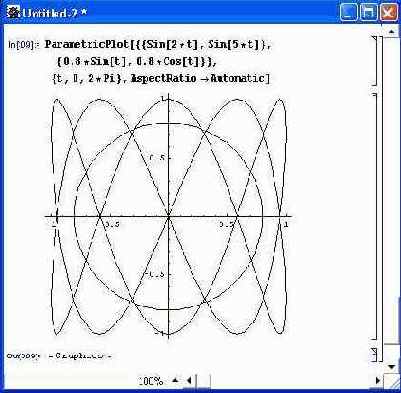
Рис. 8.13. Построение на одном графике двух фигур Лиссажу
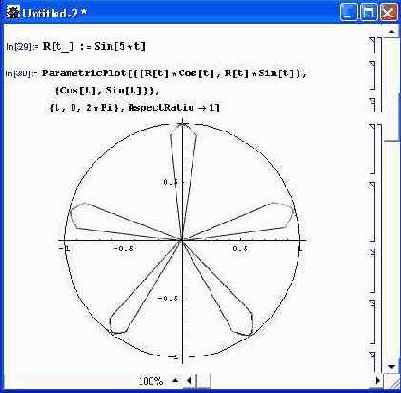
Рис. 8.14. Построение графика функции в полярной системе координат
 |
 |
 |
